Real-Time Rendering - 4th edition

Questions

What is photon mapping?
List all of the physical light/matter interaction: scattering, absorption, emission.
Seems that the book divides specular reflections between mirror reflections (perfect, BRDF is a single ray?) and glossy reflections (with a roughness > 0).
Is subsurface scattering (and in particular the radiance it causes) considered reflection? p438 “[…] plus the reflected radiance” seems to imply it.
Make a note with clear distinction, physical explanations, intuitive behaviours, dependence to light and view directions, … :
- diffuse illumination (independent of viewing angle: uniform appearance of light accross the surface, intensity of scaterred light primarly depends on angle of incidence: I suppose that is why it care about irradiance, all incoming lights will contribute, modulated by cos, to any viewing direction)
- specular illumination (create highlights, strongly view dependent: intensity is strongest along specular direction determined by the incident angle and surface normal. It cares about radiance: only the limited set of incoming directions resulting in a specular component along viewing direction are of interest.)

Feature	Specular Reflection	Diffuse Reflection
Surface Quality	Smooth surfaces	Rough surfaces
Reflection Directionality	Light is reflected in a single direction	Light is scattered in all directions
Dependence on View Angle	Highly dependent	Largely independent
Example Surfaces	Polished metal, glass, water	Matte paint, paper, unpolished wood

Effects and subset glossary

User controlled clipping planes via FS discard

Deferred shading does visibility and shading in distinct passes. It was given rise by the availability of multiple render targets (MRT) p51

Deferred shading is categorized as:

a type of rendering pipeline, and then as a class of rendering method p51.
a technique p127
a rendering scheme p500.

Parallax is the impact the observer’s viewpoint have on the observation of an object. (And apparently, the change in what is observed as the viewpoint changes).

CIE: Commission Internationale d’Eclairage.

Smoothstep and quintic equations, p181

Chapter 1 - Introduction p1

Some operators:

Binomial coefficient (i.e. “k parmi n”) $\binom{n}{k}$ = $C^k_n = \frac{n!}{k! (n-k)!}$
Unary perp dot product, noted $^\perp$, work on a vector to give another vector perpendicular to it.

Chapter 2 - The Graphics Rendering Pipeline p11

Shading is the operation of determining the effect of light on a material. It involves computing a shading equation at various points on the object.

Geometry processing p14

Model space -[model matrix]> World space -[view transform]> View (eye, camera) space -[projection matrix]-> clipping space / homogeneous clip space (clip coordinates, which are homogeneous)

In the clipping space, there is the canonical view volume (unit cube) to which the drawing primitives are clipped by the clipping stage.

Note: the projection transforms the view volume (bounded by a rectangular box (orthographic) or frustum (perspective) in view space) into the unit cube of clipping space.

After clipping, perspective division places vertices into normalized device coordinates $[-1, 1]^3$.

normalized device coordinates (NDC) -[screen mapping]-> (x, y [screen coordinates], z)[window coordinates]

Optionals:

Tesselation shader
Geometry shader
Stream output (transform feedback in OpenGL)

Rasterization p21

primitive assembly (triangle setup): Setup differentials, edge equations,…

triangle traversal: find which pixels or samples are inside a triangle, and generate fragments with interpolated properties.
A fragment is the piece of a triangle partially or fully overlapping a pixel (p49)

Pixel processing p22

Fragment shading

Merging (ROP): raster operations or blend operations. merge fragment shading output color(s) with data already present in the color buffer, handles depth buffer (z-buffer), stencil buffer. The framebuffer consists of all enabled buffers.

Chapter 3 - The Graphics Processing Unit p29

Give details of why a GPU is very efficient for graphics rendering, with details of the data-parallel architecture:

warps (nvidia) or wavefronts (amd) grouping predefined numbers of threads with the same shader program. Resident warps are said to be in flight, defining occupancy. Branching might lead to thread divergence.

Programmable shader stage has 2 types on input: uniform and varying.

Flow control is divided between static flow control based on uniforms (no thread divergence) and dynamic flow control, which depends on varyings.

A detailed history of programmable shading and graphics API p37.

Geometry shader can be used to efficiently generate cascaded shadow maps.

Stream output can be used to skin a model and then reuse transformed vertices.

The Pixel Shader p49

Multiple Render Targets (MRT) allow pixel shaders to generates distinct values and save them to distinct buffers (called Render Target). E.g. color, depth, object ids, world space distance, normals

In the context of fragment shaders, a quad is a group of 2x2 adjacent pixels, processed together to give access to gradients/derivatives (e.g. texture mipmap level selection) Gradients cannot be accessed in parts affected by dynamic flow control p51. (I suppose because each thread in a quad has to compute its part for sharing with neighbors?)

A Render Target can only be written at the pixel’s location.
Dedicated buffer type allow write access to any location. Unordered Access View (UAV) in DX / Shader Storabe Buffer Object (SSBO) in OpenGL.
Data races are mitigated via dedicated atomic units, but they might lead to stalls.

Merging stage p53

Output merger (DX) / Per-sample operations (OpenGL)

Compute shader p54

A form of GPU computing, in that it is a shader not locked into a location of the graphics pipeline. Compute shaders give explicit access to a thread ID. They are executed by thread group, all threads in the group guaranteed to run concurrently, and share a small amount of memory.

Chapter 4 - Transforms p57

Linear transforms preserve vector addition and scalar multiplication: scale, rotation
Affine transforms allow translation, they preserve parallelism of lines, but not necessarily length or angles.

For orthogonal matrices, the inverse is their transpose.

How to compute a look-at matrix p67

TODO: Note taken up-to 4.2.2 (excluded) in linear_algebra.md, to be completed.

Morphing p90

Evolution Morph Targets (Blend Shapes) p90

Projections p92

Advices to increase depth precision p100

Chapter 5 - Shading basics p103

A Shading model describes how the surface color varies based on factors such as orientation, view direction, lighting.

Some models in this chapter:

Lambertian
Gooch

Shading models that support multiple light sources will typically use one of the following structures:

\[\mathbf{c}_\text{shaded} = f_\text{unlit}(\mathbf{n}, \mathbf{v}) + \sum_{i = 0}^{n-1}{ \mathbf{c}_{\text{light}_i} f_\text{lit}(\mathbf{l}_i, \mathbf{n}, \mathbf{v}) } \text{(5.5)}\]
- More general
\[\mathbf{c}_\text{shaded} = f_\text{unlit}(\mathbf{n}, \mathbf{v}) + \sum_{i = 0}^{n-1}{ (\mathbf{l}_i \cdot \mathbf{n})^+ \mathbf{c}_{\text{light}_i} f_\text{lit}(\mathbf{l}_i, \mathbf{n}, \mathbf{v}) } \text{(5.6)}\]
- Required for physically based models
  - TODO: Why is it required? We could fold the dot product in $f_\text{lit} of equation (5.5)

Note: Varying values for materials properties (e.g. diffuse color, ambient color, …) exist in the functions $f$, even though they do not appear as explicit parameters.

The different types of light essentially describes how light vector $\mathbf{l}$ and light color $c_\text{light}$ vary over the scene. These two parameters are how light sources interact with the shading model.

Lights:

Directional light
Punctual light
- Point light (Omni light)
- Spot light

Implementing Shading Models p117

The different computations in shading have a frequency of evaluation :

Uniform frequency:
- Per installation / configuration (can even be baked in the shader)
- Valid for a few frames
- Per frame
- Per object
- Per draw call
Computed by one of the shader stages / Varying:
- Per pre-tesselation vertex: in Vertex shader (colloquially: Gouraud shading)
- Per surface patch: Hull shader
- Per post-tesselation vertex: Domain shader
- Per primitive: Geometry shader
- Per fragment: Fragment shader (colloquially: Phong shading)

Warnings: p119 Interpolation of unit vectors might have non-unit result. (-> re-normalize after interpolation)
Interpolation of differing length vector skew towards the longest. This is a problem with normals (-> normalize before interpolation), but is required for correct interpolation of directions (e.g. light)

p120: which coordinate system to choose for fragment shader computations:

World space (minimize the work for transforming e.g. lights)
View space (easy view vector, potentially better precision)
Model space (uncommon)

rendering framework, undefined, p122. I think it corresponds to our library code.

“Clamping to $[0, 1]$ is quick (often free) on GPUs” p124

Material Systems p125

The material system seems to handle the variety of materials, shading models, shaders.

A material is an artist-facing encapsulation of the visual appearance of a surface.

Shader<->Material is not a 1-to-1 correspondance.

A single material might use distinct shaders depending on the circonstances.
A shader might be shared by several materials. A usual situation is material parameterization: a material template plus parameter values produce a material instance.

“One of the most important task of a material system is dividing various shader functions into separate elements and controlling how these are combined.” p126 i.e. producing shader variants.
This has to be handled at the source code level. The larger the number of variants, the more crucial are modularity and composability.

“Typically only part of the shader is accessible to visual graph authoring.” p128

Screen-Based Antialiasing p137

Detailed overview of a lot of screen-based AA techniques (supersampling, temporal, morphological(image-based))

“Antialiasing (such as MSAA or SSAA) is resolved by default with a box filter” p142 (and it seems to mean taking the average color). TODO: I do not understand why, since it seems box would just pick nearest…

Transparency, Alpha, Compositing p148

Transparency:

alpha to coverage ?
stochastic transparency ?
alpha blending “alpha simulates how much the material covers the pixel” p151 (MSAA samples might already handle the fragment geometric coverage of the pixel).

Blend modes: usual is over when rendering transparent objects back to front, and there is also under (apparently only when rendering front to back?)

order independent transparency (OIT):

Depth peeling
A-buffer
Multi-layer alpha blending
Weighted sum and Weighted average

Pre-multiplied alphas (or associated alphas) are making the over operator more efficient, and make it possible to use over and additive blending within the same blend state.

Display encoding p160

Displays have a (standardised) electrical-optical transfer function (EOTF) (or display transfer function): it defines the relationship between the electric level of the signal and emitted radiance level (I assume the electric level is linear with the digital value in the color buffer).

Since our computations are done in linear (radiance) space, we need to apply the inverse of the EOTF to the final value written in the color buffer. This way, the display will cancel it with the forward EOTF, and the expected radiance is displayed. (This process of nullifying the display’s non-linear response curve is called gamma correction, or gamma encoding, or gamma compression, since the EOTF is about $y = x^{\gamma}$)

“Luckily”, human radiance sensitivity is close to the EOTF inverse. (Note: this human sensitivity is not what gamma correction corrects.)
Thanks to that, the encoding is roughly perceptually uniform :
we perceive about the same difference between two encoded levels everywhere in encoded space, even though the absolute radiance difference is much smaller for smaller encoded values (in other words, the EOTF mitigates banding).

Encoding is also called gamma compression. It is a form of compression that preserves the perceptual effect over the limited precision of the color buffer better than if there was no encoding (banding would be more servere for small radiance values)
Put another way, There is linear value used for physical computations, and display-encoded values (e.g. displayable image formats). We need to move data to(encode) or from(decode) the display-encoded form to either display it, or read images values for computations.

sRGB defines the EOTF for consummer monitor displays. It is closely approximated by $\gamma = 2.2$.

Note: a display does transform a sRGB non-linearly encoded image to linear radiance values. So the forward EOTF should be applied to linearize an image format that is sRGB encoded.

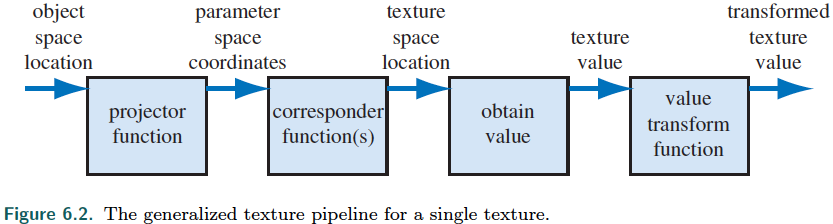
Chapter 6 - Texturing p169

texture mapping is assigning to a point (usually in model space) its textures coordinates.
Note: texture coordinates (usually $[0,1]^2$) are distinct from texture space location (in the case on an image, it could be the pixel position)

Wang tiles: small set of square tiles with matching edges.

Texels have integer coordinates (do they mean indices?). In OpenGL, and since DX10, the center of a texel has coordinates (0.5, 0.5). Origin is lower-left (OpenGL) or upper-left (DX).

dependant texture read mean fragment shader has to “compute” the texture coordinates instead of using the (u, v) passed from the VS verbatim. There is an older, more specific definition: a texture read whose coordinates are dependent upon another texture read.

power-of-two (POT) textures are $2^m \times 2^n$ texels. Opposed to NPOT.

detail textures can be overlaid on magnified textures (cf Blending and filtering materials)

mipmap chain: set of images constituting all levels of a mipmapped texture. The continuous coordinate $d$, or texture level of detail, is the parameter determining where to sample in the levels of a mipmap chain (along the mipmap pyramid axis). OpenGL calls it $\lambda$.

The goal is a pixel-to-texel of at least 1:1 (so sampling (pixels) is at least twice the max signal frequency (1/2texels)).
$(u, v, d)$ triplet allows for trilinear interpolation.
A level of detail bias (LOD bias) can be added to $d$ before sampling.

A major limitation of mipmaps is overblurring, because the filtering is isotropic (but the pixel backprojection into texture space can be far from a square).

anisotropic filtering: Summed-Area Table (SAT) p186
Unconstrained Anisotropic Filtering (in modern GPUs) p188
Elliptical Weighted Area (EWA) is a hight quality software approach.

cube maps p190

Texture compression p192

S3 texture compression (S3TC) chosen as a standard in DX under the name DXTC or BC. De facto OpenGL standard.
Ericson Texture Compression (ETC) p194, used in OpenGL ES (and GL 4). One component variant Ericson Alpha Compression.
Variants for normal compression p195
- Adaptative Scalable Texture Compression (ASTC) p196.
  All variants have data compression assymetry, decoding can be orders of magnitude faster than encoding.

There are approaches to reduce banding (e.g. histogram renormalization) p196

Procedural Texturing p198

Noise function sampled at successive power-of-two frequencies (octaves), weighted and summed to obtain a turbulence function. (Note wavelet noise improves on Perlin noise).

Material mapping p201

The idea is when using Material Parametrization, to fetch parameter values from textures. Further, the texture value could control the dynamic flow of a shader, selecting different shading equations.
Warning: shading model inputs with a linear relationship to output color (e.g. albedo) can be filtered with standard techniques. This is not the case for non-linear (roughness, normals,…)

Alpha-mapping p202

The alpha value can be used for alpha-blending (blend stage) or alpha-testing(discard) Used for decaling, cutouts (e.g. cross-tree, billboarding), Alpha-test has to take special care wrt mipmapping p204

Alpha-to-coverage translates transparency as a MSAA coverage mask p207
Attention: linear interpolation treat RGBA as premultiplied (which is usually not the case). A workaround is to paint transparent pixels p208

Appearance modeling (Ch 9 p367) assumes different scales of observations, influencing modelling approaches:

Macroscale (large scale, usually several pixels), as triangles
Mesosclae (middle scale, 1 to a few pixels), as textures, e.g. normal maps
Microscale (smaller than a pixel), encapsulated in the shading model, e.g. via the BRDF (Chapter 9)
Nanoscale ($[1, 100]$ wavelengths in size, unusual in real-time), by using wave optics models (Chapter 9)

Bump-mapping p208

A family of small-scale (meso-feature) detail representation, essentially modifying the shading normal at fragment location.
The frame of reference of the normal map is usual surface space, with a TBN matrix to change from object to surface.

Note: p210 “in [the case of textures mirrored on symmetric objects], the handedness of the tangent space will be different on the two side”. I think this is because the normal map will be applied on both sides, and to actually mirror the resulting normal we need to mirror the TBN basis (which changes its handedness). Also, from Assimp doc: “The (bi)tangent of a vertex point in the direction of the positive X(Y) texture axis”. This also implies mirroring the TBN basis when texture is mirrored.

Types of bump mapping:

Blinn’s method p211, via offset vector bump map (offset map) or height map
Normal mapping, via a normal map (difficult to filter: the normal-map values have a non-linear relationship to the shaded color.):
- Initially in world-space. Trivial to use, but objects cannot be rotated.
- object-space allows rotation, but bind the map to a specific surface on a specific object (i.e. limit reuse).
- tangent-space is the usual approach, but requires computing the TBN.

Horizon mapping allows bumps to cast shadows onto their own surface.

Parallax mapping p214

Parallax mapping in general aims to determine what is seen at a pixel using a heightfield. It can give better occlusion/shadow clues.

Approaches:

Parallax mapping is an euristic (and cheap) approach that offsets texture coordinates before sampling the albedo.
Parallax occlusion mapping (POM) or relief mapping use ray marching along the view vector to find a better intersection with the heightfield. This approach can be extended with self-shadowing.
Shell mapping p220 approach allows to render silouhette edges of objects (otherwise showing the underlying primitive straight edge).

Textured lights p221

Projective textures (called light attenuation textures in this context) can be used to modulate the light intensity of lights (limited to a cone or frustum for normal texture, or all directions for cubemap).
They are then called gobo or cookie lights (the textures are light attenuation mask, or gobo maps, or cookie textures)

Chapter 7 - Shadows p223

Occluders cast shadows on receivers.

Shadows are umbra + penumbra.

Hard shadows do not have a penumbra
Soft shadows have a penumbra

Planar shadows p225

Planar shadows are a simple case where the shadows are cast on a planar surface.
Idea to use stencil buffer to limit drawing shadows to a surface p227.

A light map is a texture that modulate the intensity of the underlying surface (e.g. planar shadow rendered to a texture).

Heckbert and Herf’s method p228 can be used offline to generate “ground-truth” shadows. It can be extended to work with any algorithm producing hard-shadows.

Shadow volume p230

Shadow volumes are analytical, not image based, so they avoid sampling problems. They have unpredictable costs.

Shadow Maps p234

Shadow map (shadow depth map, shadow buffer) is the content of a z-buffer rendered from the light perspective.\

Omnidirectional shadow maps capture the z-buffer all-around the light, typically via a six-view cube.

Prone to self-shadow aliasing (surface acne, shadow acne).
Mitigated via a bias factor, which is more effective when proportional to the angle between receiver and light: slope scale bias. Too much bias introduces light leaks (Peter Panning).

Second-depth shadow mapping renders only backfaces to the shadow map.

Resolution enhancement p240

Resolution enhancement methods aim to address aliasing.

Perspective aliasing is the mismatch in coverage between the color-buffer pixels and texels in the shadow map (ideal ratio would be 1:1), usually due to foreshortening occurring in the perspective view. It tends to show as “jagged” shadows.
Projective aliasing is due to surfaces forming a steep angle with the light direction, but are seen face one.

Perspective warping techniques attempt to better match the light’s sampling rates to the eye’s, usually altering the light’s view plane (via its matrix) so its sample distribution gets closers to the color-buffer (eye) samples:

Perspective shadow maps (PSM)
Trapezoidal shadow maps (TSM)
Light space perspective shadow maps (LiSPSM).

Those tend to fail with dueling frusta (deer in the headlights): i.e. when a light in front of the camera is facing at it.
Additional problems such as sudden changes in quality had perspective warping fall out of favor.

Another approach it to generate several shadow maps for a given view. The popular approach is cascaded shadow maps (CSM), also called parallel-split shadow maps. It requires z-partitioning along the view.\

sample distribution shadow maps (SDSM) use previous frame z-depth to refine partitioning.

Percentage-closer Filtering p247

Percentage-closer filtering (PCF) provides an approximation of soft-shadows by comparing the depth to several texels in the shadow-map, returning an interpolation of the individual results.

Percentage-closer soft shadows (PCSS) p250 aim for more accurate soft-shadows by sampling the shadow map to find possible occluders to vary the area of neighbours that will be sampled in the shadow map. This allows contact hardening.
Enhancements are contact hardening shadows (CHS), separable soft shadow mapping (SSSM), min/max shadow map.

Filtered Shadow Maps p252

variance shadow map (VSM) allow filtering (blur, mipmap, summed area tables,…) the shadow maps. This is efficient for rendering large penumbras. It suffers from light bleeding for overlapping occluders.

Other approaches to filtered shadow maps are convolution shadow maps , exponential shadow map ESM (or exponential variance shadow map EVSM), moment shadow mapping.

Volumetric Shadow Techniques p257

deep shadow maps, opacity shadow maps, adaptive volumetric shadow maps

Other Applications p262

screen-space shadows ray march the camera’s depth buffer treated as an height field. (Good for faces, where small feature shadows are important)

Other analytical approaches:

Ray tracing
Irregular z-buffer (IZB) p259 gives precise hard shadows.

Chapter 8 - Light and Color

Our perception of color is a psychophysical phenomenon: a psychological perception of physical stimuli.

Radiometry is about measuring electromagnetic radiation.
Photometry deals with light values weighted by the sensitivity of the human eye.
Colorimetry deals with the relationship between spectral power distribution and the perception of colors.

Radiometry p267

radiant flux $\Phi$ in watts (W): flow of radiant energy over time.
irradiance $E = d\Phi / dA$ in W/m².
radiant intensity $I = d\Phi / d\omega$ in W/sr, flux density per direction (solid angle)
radiance $L = d^2\Phi/ (dA d\omega)$ in W/(m² sr), measure electromagnetic radiation in a single ray: the density of radiant flux with respect to both area and solid angle. It is what sensors (eye, camera, …) measure. The area is measured in a plane perpendicular to the ray (“projected area”).

radiance distribution describes all light travelling anywhere in space. In lighting equation, radiance at point $\mathbf{x}$ along direction $\mathbf{d}$ often appears as $L_o(x, d)$ (going out) or $L_i(x,d)$ (entering). By convention $\mathbf{d}$ always points away from $\mathbf{x}$.

spectral power distribution SPD is a plot showing how energy is distributed across wavelength.

All radiometric quantities have spectral distributions.

Photometry

Each radometric quantity has an equivalent photometric quantity (the differences are the CIE photometric curve used for conversion, and units of measurement)

luminous flux in lumen (lm)
illuminance in lux (lx)
luminous intensity in candela (cd)
luminance in nit = cd/m²

Colorimetry p272

CIE’s XYZ coordinates define a color’s chromaticity and luminance. chromaticity diagram, e.g; CIE 1931 taken by projection on the X+Y+Z=1 plane, is the lobe with the curved outline being the visible spectrum, with the straight line at the bottom called the purple line. The white point define the achromatic stimulus. More perceptually uniform diagrams are developped, such as CIE 1976 UCS (part of the CIELUV color space). A triangle in the chromaticity diagram represent the gamut of a color space, with vertices being the primaries. Given a $(x, y)$ color point on the chromaticity diagram and drawing a line with the white point give the excitation purity (~= saturation) as relative distance from the point to the edge, and the dominant wavelength (~= hue) as the intersection with the edge.

spectral reflectance curve describes how much of each wavelength a surface reflects.

Scene to screen p281

A display standard, such as sRGB, seems to encompass both a color-space (a RGB gamut defined by primitive colors, and a whitepoint) and display encoding function/curve. Also white luminance level (cd/m²).

HDR

Dynamic range is about luminance?

Perceptual quantizer (PQ) and hybrid log-gamma (HLG) are non-linear display encodings defined by Rec. 2100 display standard.

tone mapping or tone reproduction is the process converting scene radiance values to display radiance values . The applied transform is called the end-to-end transfer function or scene-to-screen transform. It transform the image state from scene-referred to display-referred. Imaging pipeline:

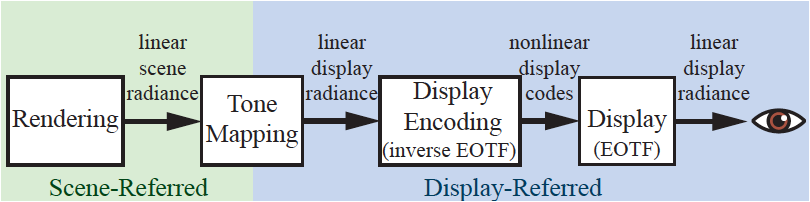
Tone mapping can be seen as an instance of image reproduction: its goal is to create a display-referred images reproducing at-best the perceptual impression of observing the original scene.

Image reproduction is challenging: luminance of scene exceeds display capabilities by orders of magnitudes, and saturation of some colors are far out the display gamut. It is achieved by leveraging properties of the human visual system:

adaptation: compensation for differences in absolute luminance.

exposure in rendering is a linear scaling on the scene-referred image before tone reproduction transform.

global tone mapping (scaling by exposure then applying tone reproduction transform) where the same mapping is applied to all pixels, vs local tone mapping with different mappings based on surrounding pixels.

color grading manipulates image colors with the intention to make it look better in some sense. It is a form of preferred image reproduction.

Chapter 9 - Physically Based Shading p293

TODO: clarify the list of physical interactions between light and matter, and their classification. Is it reflection, transmission and absorption? In particular, how to classify refraction compared to transmission. Is refraction a separate effect occuring on transmitted light?

From “Entretien avec Luc, 02/06/2024”: the only physical interaction between photons and matter should be scattering. TODO: Maybe absorption is the another interaction?

Light-matter interaction: the oscillating electrical field of light causes the electrical charges in matter to oscillate in turn. Oscillating charges emit new light waves, redirecting some energy of the incoming light wave in new direction. This reaction is scaterring (fr: diffusion) (usually, same frequency). An isolated molecule scatters in all directions, with directional variation in intensity.

Particles smaller than a wavelength scatter light with constructive interference. Particles beyond the size of a wavelength do not scatter in phase, the scattering increasingly favors the forward direction and the wavelength dependency decrease.

In homogeneous medium, scattered waves interfere destructively in all direction except the original direction of propagation. The ratio of phase velocities defines the index of refraction IOR $n$. Some media are absorptive, decreasing the wave applitude exponentially with distance. The rate is defined by the attenuation index $\kappa$. Those two optical properties are often combined into a single complex number $n + i\kappa$, the complex index of refraction.

A planar surface separating different indices of refraction scatter light a specific way: transmitted wave and reflected wave.

Transmitted wave is refracted at an angle $\theta_t$, following Snell’s law: $\sin(\theta_t) = \frac{n_1}{n_2} \sin(\theta_i)$

In geometrical optics light is modeled as rays instead of waves, and surfaces irregularities ar much smaller or much larger than wavelength.

On the other hand, when irregularities are in the range 1-100 wavelengths, diffractions occurs.

microgeometry are surface irregularities too small to be individually rendered (i.e. smaller than a pixel). For rendering, microgeometry is treated statistically via the roughness.

subsurface scattering p305

local subsurface scattering can be used when the entry-exit distance is smaller than the shading scale. This local model should separate the specular term for surface reflection from diffuse term for local subsurface scattering.
global subsurface scattering is needed when the distance is larger than the shading scale (the inter-samples distance).

Camera p307

Sensors measure irradiance over their surface. Added enclosure, aperture and lens combine effect to make the sensor directionally specific, so the system now measures radiance.

BRDF p309

The ultimate goal of physically based rendering is to compute $L_i(\mathbf{c}, -\mathbf{v})$ for the set of view rays $\mathbf{v}$ entering the camera positioned at $\mathbf{c}$.

participating media does affect the radiance of a ray via absorption or scattering.

Without participating media (i.e. in clean air, commonly assumed in rendering), given $\mathbf{p}$ is the intersection of the view ray with the closest object surface: $L_i(\mathbf{c}, -\mathbf{v}) = L_o(\mathbf{p}, \mathbf{v})$

The goal is now to calculate $L_o(\mathbf{p}, \mathbf{v})$. We limit the discussion to local reflectance phenomena (no transparency, no global subsurface scattering), i.e. light received and redirected outward by the currently shaded point only:

surface reflection
local subsurface scattering

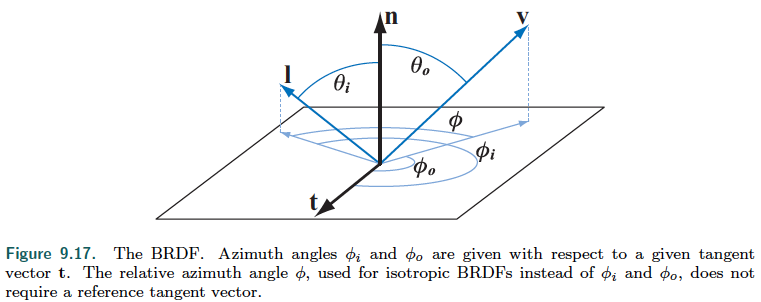
Local reflectance is quantified by the bidirectional reflectance distribution function BRDF. BRDF only depends on incoming light direction $\mathbf{l}$ and outgoing view direction $\mathbf{v}$, and is noted $f(\mathbf{l}, \mathbf{v})$. BRDF is often used to mean the spatially varying BRDF SVBRDF (capturing the variation of the BRDF based on spatial location on the surface).

A general BRDF at a given point has four parameter, elevations $\theta_i, \theta_o$, azymuths $\phi_i, \phi_o$.
Isotropic BRDF remains the same for a given azimuth difference between incoming and outgoing ray (i.e. not affected by a rotation of the surface around the normal). It can be reduced to 3 parameters elevations $\theta_i, \theta_o$, azymuth difference $\phi$.

BRDF varies based on wavelength. For real-time rendering the BRDF returns a spectral distribution as an RGB triples.

Reflectance equation, with $\Omega$ the hemisphere above the surface centered on $\mathbf{n}$: $L_o(\mathbf{p}, \mathbf{v}) = \int_{\mathbf{l} \in \Omega}{f(\mathbf{l}, \mathbf{v}) L_i(\mathbf{p}, \mathbf{l}) (\mathbf{n} \cdot \mathbf{l}) d\mathbf{l}} \qquad\text{(9.3)}$

Note: $p$ is often omitted from the notation, giving equation $\text{(9.4)}$.

BRDF physical properties:

Helmoltz reciprocity $f(\mathbf{l}, \mathbf{v}) = f(\mathbf{v}, \mathbf{l})$ (often violated by renderers). Can be used to assert a BRDF physical plausibility.
conservation of energy outgoing energy cannot exceed incoming energy.

directional-hemispherical reflectance can measure to what degree a BRDF is energy conserving. It measures the amount of light, coming from a single direction $\mathbf{l}$, reflected over all directions: $R(\mathbf{l}) = \int_{\mathbf{v} \in \Omega} {f(\mathbf{l}, \mathbf{v}) (\mathbf{n} \cdot \mathbf{v}) d\mathbf{v}}$

hemispherical-directional reflectance measure the amount of light, coming from all directions of the hemisphere, that is reflected toward a given direction $\mathbf{v}$:

\[R(\mathbf{v}) = \int_{\mathbf{l} \in \Omega} {f(\mathbf{l}, \mathbf{v}) (\mathbf{n} \cdot \mathbf{l}) d\mathbf{l}}\]

For a reciprocal BRDF, directional-hemispherical reflectance is equal to the hemispherical-directional reflectance. In this situation, directional albedo is a blanket term for both, they can be used interchangeably.

Note: For a BRDF to be energy conserving, $R(\mathbf{l})$ is in the range $[0, 1]$ for any $\mathbf{l}$, but the BRDF does not have this restriction and can go above $1$.

A Lambertian BRDF p313 has a constant value (independent of incoming direction $\mathbf{l}$). So does the directional-hemispherical reflectance, whose constant value is called diffuse color $\mathbf{c}{diff}$ or the _albedo $\rho$ (or in this chapter, subsurface albedo $\rho_\text{ss})$: $R(\mathbf{l}) = \pi f(\mathbf{l}, \mathbf{v}) = \rho_\text{ss}$ $f(\mathbf{l}, \mathbf{v}) = \frac{\rho_\text{ss}}{\pi}$

TODO: derive that $\int_{\mathbf{l} \in \Omega} (\mathbf{n} \cdot \mathbf{l}) d\mathbf{l}$ is $\pi$.

Illumination p315

$L_i(\mathbf{l})$ term in the reflectance equation is the incoming light from all directions.

Global illumination calculates $L_i(\mathbf{l})$ by simulating how light propagates and reflects throughout the scene, by using the rendering equation

Note: The reflectance equation is a special case of the rendering equation.

Local illumination algorithms uses the reflectance equation to compute shading locally at each surface point, and are given $L_i(\mathbf{l})$ as input which does not need to be computed.

We can define a light color $\mathbf{c}_{light}$ as the reflected radiance from a white Lambertian surface facing toward the light ($\mathbf{n} = \mathbf{l}$)

TODO: does it mean $L_i(l) = \mathbf{c}_\text{light}$ ? Seems implied by the simplified reflectance equation. Plus radiance is indeed denoted by $L$.

In the case of directional and punctual lights and local illumination (i.e. direct light contribution), each surface point $\mathbf{p}$ receive (at most) a single ray from each light source, along direction $\mathbf{l}_c$, simplifying the reflectance equation to: $L_o(\mathbf{v}) = \pi f(\mathbf{l}_c, \mathbf{v}) \mathbf{c}_{light} (\mathbf{n} \cdot \mathbf{l}_c)$

Clamping the dot product to zero to discard lights under the surface, the resulting contribution for $n$ lights is: $L_o(\mathbf{v}) = \pi \sum_{i=1}^{n} f(\mathbf{l}_{c_i}, \mathbf{v}) \mathbf{c}_{light_i} (\mathbf{n} \cdot \mathbf{l}_{c_i})^+$ Note: this ressembles equation (5.6) p109, with $\pi$ cancelled out by the $/\pi$ often appearing in the BRDFs.

On to a specific phenomena: Fresnel reflectance p316

Fresnel equations are complex and not presented in the chapter.

Light incident on flat surface splits into a reflected part and a refracted part. The direction of reflection $\mathbf{r}_i$ forms the same angle $\theta_i$ with the surface normal $\mathbf{n}$ as $\mathbf{l}$ does: $\mathbf{r}_i = 2 (\mathbf{n} \cdot \mathbf{l}) \mathbf{n} - \mathbf{l}$

Fresnel reflectance $F$ is the amount of light reflected (as a fraction of incoming light, i.e. a reflectance). It depends on $\theta_i, n_1, n_2$.

External reflection (e.g. “air to material”) when $n_1 < n_2$, internal reflection when $n_1 > n_2$.

Characteristics of $F(\theta_i)$ for a given substance interface:

At normal incidence ($\theta_i = 0°$), the value is is a property of the substance, noted $F_0$ : the normal-incidence Fresnel reflectance. It can be seen as the characteristic specular color of this substance.
As $\theta_i$ increases, $F(\theta_i)$ tend to increase, reaching a value of $1$ for all frequencies (white) at $\theta_i = 90°$. This increase in reflectance at glancing angles is often called the Fresnel effect.

An approximation of the complex equation for Fresnel reflectance is given by Schlick: $F(\mathbf{n}, \mathbf{l}) \approx F_0 + (1 - F_0) (1 - (\mathbf{n} \cdot \mathbf{l})^+)^5$

Pointers to other approximations are given p320, or the option to use other powers than $5$.

A more general form of the Schlick approximation, giving control over the color at 90° $F_{90}$: $F(\mathbf{n}, \mathbf{l}) \approx F_0 + (F_{90} - F_0) (1 - (\mathbf{n} \cdot \mathbf{l})^+)^{\frac{1}{p}}$

Dielectrics (insulators) have low $F_0$, which makes the Fresnel effect especially visible. Their optical properties rarely varies over the visible spectrum.
Metals have a high $F_0$ (usually above 0.5), which is colored. They immediately absorb any transmitted light: they do not exhibit subsurface scattering or transparency. So all the visible color comes from $F_0$.
Semiconductors have $F_0$ in between, but are rarely needed to render. Usually, the range [0.2, 0.45] is avoided for practical realistic purposes.

Parameterizing Fresnel values p324 discusses parameters of PBR models.

From the observation that metals have no diffuse color, and that dielectrics have a restricted set of possible $F_0$ values: an often-used parameterization combines specular color $F_0$ and diffuse color $\rho_\text{ss}$, parameters being an RGB surface color $\mathbf{c}\text{surf}$ and a scalar _metalness $m$.

If $m = 1$, $F_0$ is set to $\mathbf{c}\text{surf}$, $\rho{ss}$ is set to black.
If $m = 0$, $F_0$ is set to a plausible dielectric value (e.g. 0.04, or another param), $\rho_\text{ss}$ is set to $\mathbf{c}_\text{surf}$

Metalness has some drawbacks:

cannot express some types of materials, such a coated dielectrics with tinted $F_0$.
artifacts can occur on the boundaries between metal and dielectric.

Parameterization trick: since $F_0$ lower than 0.02 are very unusual, low values can be reserved for a specular occlusion mask, to suppress specular highlights in cavities.

Internal reflection p325

When $n_1 > n_2$, then $\theta_t > \theta_i$. So a critical angle $\theta_c$ exists where no transmission occurs: all incoming light is reflected. This phenomenon is total internal reflection occurring when $\theta_i > \theta_c$.

$F(\theta_i)$ curve for internal reflection is a “compressed” version of the curve for external reflection, with the same $F_0$ and perfect reflectance reached at $\theta_c$ instead of 90°.

It can occur in dielectrics (not metals which absorb), which have real-valued refractive indices: $\sin \theta_c = \frac{n_2}{n_1} = \frac{1 - \sqrt{F_0}}{1 + \sqrt{F_0}}$

Microgeometry p327

Microgeometry models surface irregularities that are smaller than a pixel, but larger than 100 wavelengths. Most surfaces have an isotropic distribution of the microscale surface normals (i.e. rotationally symmetrical).

Effects of microgeometry on reflectance:

multiple surface normals
Shadowing: the occlusion of the light source by microscale surface details. -> hidden form $\mathbf{l}$.
Masking: some facets hiding others from the point of view. -> hidden form $\mathbf{v}$
Interreflection: light may undergo multiple boundes before reaching the eye.
- subtle in dielectrics, light is attenuated by the Fresnel reflectance at each bounce.
- source of any visible diffuse reflection in metals (I do not understand why the distribution of normals is not also a source of diffuse reflection?), since metals do no exhibit subsurface scattering. They are more deeply colored than primary reflection, since they result from light interacting multiple times with the surface.

For all surfaces types, visible size of irregularities decresses as angle to the normal $\theta_i$ increases. This combines with the Fresnel effect to make surfaces appear highly reflective at glancing angles (lighting and viewing).

TODO: classify the different types of reflections, and define generic reflection. The book differentiates specular reflectance (“surface reflectance”) from subsurface reflectance (I suppose diffuse reflectance) p330.
This is consistent with what appears on wikipedia Specular reflection vs Diffuse reflection.

Microscale surface details can also affect subsurface reflectance. If microgeometry irregularities are larger than subsurface scattering distance, their shadowing and masking can cause retroreflection: “where light is preferentially reflected back toward its incoming direction” p330.

Microfacet theory p 331

Microfacet theory is a mathematical analysis of the effects of microgeometry on reflectance, on which many BRDF models are based. The theory is based on the modeling of microgeometry as a collection of microfacets:

each is flat, with a single normal $\mathbf{m}$.
each individually reflects light according to the micro-BRDF $f_\mu(\mathbf{l}, \mathbf{v}, \mathbf{m})$. Their combined reflectances add up to the overall surface BRDF.

The model has to define the statistical distribution of microfacet normals:

$D(\mathbf{m})$ is the normal distribution function NDF (or distribution of normals). It tells us how many of the microfacets have normals pointing in certain directions.
$G_1(\mathbf{m}, \mathbf{v})$ is the masking function, the fraction of microfacets with normal $\mathbf{m}$ that are visible along view vector $\mathbf{v}$. (note: does not address shadowing).
The product $G_1(\mathbf{m}, \mathbf{v})D(\mathbf{m})$ is the distribution of visible normals.

The projections of the microsurface and macrosurface onto the plane perpendicular to any view direction are equal:

$\int_{m \in \Theta} D(\mathbf{m})(\mathbf{v} \cdot \mathbf{m}) d\mathbf{m} = \mathbf{v} \cdot \mathbf{n} \text{, dot products under integration are NOT clamped to 0 (9.22)}$ $\int_{m \in \Theta} G_1(\mathbf{m}, \mathbf{v}) D(\mathbf{m})(\mathbf{v} \cdot \mathbf{m})^+ d\mathbf{m} = \mathbf{v} \cdot \mathbf{n} \text{, dot products ARE clamped to 0 (9.23)}$

Heitz solved the dilemma (for now) as to which $G_1$ to use. From the masking function proposed in the litterature, only two satisfy equation 9.23:

Torrance-Sparrow “V-cavity”.
Smith masking function.
- Closer match to behavior of random microsurfaces than Torrance-Sparrow.
- normal-masking independance: does not depends on the direction of $\mathbf{m}$ as long as it is frontfacing.
- drawbacks:
  - theoretically not consistent with structure of actual surfaces
  - practically, it is quite accurate for random surfaces, but less when there is a strong dependency between normal direction and masking.

Smith $G_1$: $G_1(\mathbf{m}, \mathbf{v}) = \frac{\chi^+(\mathbf{m} \cdot \mathbf{v})}{1 + \Lambda(\mathbf{v})}$ with:

$\chi^+(x)$ the positive characteristic function: 1 when $x > 0$, 0 when $x \leq 0$.
$\Lambda$ function differing for each NDF.

From those elements, the overall macrosurface BRDF can be derived: $f(\mathbf{l}, \mathbf{v}) = \int_{m \in \Omega} f_\mu(\mathbf{l}, \mathbf{v}, \mathbf{m}) G_2(\mathbf{l}, \mathbf{v}, \mathbf{m}) D(\mathbf{m}) \frac{(\mathbf{m} \cdot \mathbf{l})^+}{|\mathbf{n} \cdot \mathbf{l}|} \frac{(\mathbf{m} \cdot \mathbf{v})^+}{|\mathbf{n} \cdot \mathbf{v}|} d\mathbf{m} \qquad \text{(9.26) p334}$

TODO: Get an intuition of for the two dot product ratios?

$G_2(\mathbf{l}, \mathbf{v}, \mathbf{m})$ is the joint masking-shadowing function. It derives from $G_1$, and accounts for masking as well as shadowing (but not interreflection), giving the fraction of microfacets with normal $\mathbf{m}$ that are visible from two directions:

view vector $\mathbf{v}$
light vector $\mathbf{l}$

Several forms of $G_2$ are given p335. Heitz recommends the Smith height-correlated masking-shadowing function: $G_2(\mathbf{l}, \mathbf{v}, \mathbf{m}) = \frac{\chi^+(\mathbf{m} \cdot \mathbf{v}) \chi^+(\mathbf{m} \cdot \mathbf{l})} {1 + \Lambda(\mathbf{v}) + \Lambda(\mathbf{l})}$

For rendering, the general microfacet BRDF $\text{(9.26)}$ is used to derive a closed-form solution given a specific choice of micro-BRDF $f_\mu$.

BRDF models for surface reflection p336

With few exceptions, specular BRDF terms used in PBR are derived from microfacet theory.

The half vector $\mathbf{h}$ is given by: $\mathbf{h} = \frac{\mathbf{l} + \mathbf{v}}{||\mathbf{l} + \mathbf{v}||}$

In the case of specular reflection, each microfacet is a perflectly smooth Fresnel mirror (reflect each incoming ray in a single reflected direction). So, $f_\mu(\mathbf{l}, \mathbf{v}, \mathbf{m})$ is zero unless $\mathbf{m}$ is aligned with $\mathbf{h}$.

This collapses the integral into an evaluation of the integrated function at $\mathbf{m} = \mathbf{h}$: $f_{\text{spec}}(\mathbf{l}, \mathbf{v}) = \frac{ F(\mathbf{h}, \mathbf{l}) G_2(\mathbf{l}, \mathbf{v}, \mathbf{h}) D(\mathbf{h}) } { 4 |\mathbf{n} \cdot \mathbf{l}| |\mathbf{n} \cdot \mathbf{v}| }$

TODO: is $F(\mathbf{h}, \mathbf{l})$ used as the micro-BRDF $f_\mu(\mathbf{l}, \mathbf{v}, \mathbf{m})$? It would make some sense, since the microfacet are perfect mirrors (their whole contribution is the reflectance).

Note: the book points at optimization to avoid calculating $\mathbf{h}$ and to remove $\chi^+$ p337.

Now formulas for the NDF $D$ and the masking-shadowing function $G_2$ must be found.

Normal Distribution Functions p337

The shape of the NDF determines the width and shape of the cone of reflected rays (i.e. the specular lobe), which determines the size and shape of specular highlights.

Isotropic NDF p338

An isotropic NDF is shape-invariant if the effect of its roughness parameter is equivalent to scaling the microsurface.

An arbitrary isotropic NDF has a $\Lambda$ function depending on two variables, roughness $\alpha$ and incidence angle.
For a shape-invariant NDF, $\Lambda$ only depends on variable $a$ (with $\mathbf{s}$ replaced by either $\mathbf{v}$ or $\mathbf{l})$: $a = \frac{\mathbf{n} \cdot \mathbf{s}}{\alpha \sqrt{1 - (\mathbf{n} \cdot \mathbf{s})^2}}$

Isotropic Normal Distribution Functions:

Beckmann NDF p338 (first microfacet model developed by the optics community) is chosen for the Cook-Torrance BRDF. The NDF is shape-invariant.
Blinn-Phong NDF p339 (less expensive to compute than others) was derived by Blinn as a modification of the (non physically based) Phong shading model. $D(\mathbf{m}) = \chi^+(\mathbf{n} \cdot \mathbf{m}) \frac{\alpha_p + 2}{2 \pi} (\mathbf{n} \cdot \mathbf{m})^{\alpha_p}$
- $\alpha_p$ is the roughness parameter of the Blinn-Phong NDF (higher is smoother).
  - Since it is visual impact is highly non-uniform, its is often mapped non-linearly to a user-manipulated parameter, such as $s \in [0, 1]$ in $\alpha_p = m^s$ with constant $m$ being the upper-bound (e.g. 8192).
  - Equivalent values for the Beckmann and Blinn-Phong roughnesses are found using $ \alpha_p = 2 \alpha_b^{-2} - 2$.
- It is not shape-invariant, and an analytic form for its $\Lambda$ function does not exist.
  - Walter et al. suggest using the Beckmann $\Lambda$ with the parameter equivalent function above.
Trowbridge-Reitz distribution NDF p340(recommended by Blinn in a 1977 paper) was rediscovered by Walter et al. who named it GGX distribution, which is now the common name. $D(\mathbf{m}) = \frac{ \chi^+(\mathbf{n} \cdot \mathbf{m}) \alpha_g^2 } { \pi (1 + (\mathbf{n} \cdot \mathbf{m})^2 (\alpha_g^2 - 1))^2 }$
- $\alpha_g$ roughness control is similar to that provided by Beckmann $\alpha_b$.
  - In the Disney principled shading model, the user-manipulated roughness parameter $r \in [0, 1]$ maps as $\alpha_g = r^2$. It has a more linear visual effect, and is widely adopted.
- It is shape-invariant, with a relatively simple $\Lambda$: $\Lambda(a) = \frac{-1 + \sqrt{1 + \frac{1}{a^2}}}{2}$
  - note: $a$ only appears squared, which avoids a squareroot to compute it.
- the popularity of GGX distribution and Smith masking-shadowing function has lead to several optimizations for combination of the two p341. Notably: $\frac {G_2(\mathbf{l}, \mathbf{v})} {4|\mathbf{n} \cdot \mathbf{l}||\mathbf{n} \cdot \mathbf{v}|} \Longrightarrow$ $\frac {0.5} { (\mathbf{n} \cdot \mathbf{v})^+ \sqrt{\alpha_g^2 + (\mathbf{n} \cdot \mathbf{l})^+ ((\mathbf{n} \cdot \mathbf{l})^+ - \alpha_g^2 (\mathbf{n} \cdot \mathbf{l})^+)} + (\mathbf{n} \cdot \mathbf{l})^+ \sqrt{\alpha_g^2 + (\mathbf{n} \cdot \mathbf{v})^+ ((\mathbf{n} \cdot \mathbf{v})^+ - \alpha_g^2 (\mathbf{n} \cdot \mathbf{v})^+)} } \qquad \text{(9.43)}$
generalized Throwbridge-Reitz (GTR) p342 NDF goal is to allow more control over the NDF’s shape (specifically the tail). It is not shape-invariant.
Student’s t-distribution STD and exponential poweer distribution EPD p343 are shape invariant, and quite new (unclear if they will find use atm).

An alternative to increasing NDF complexity is to use multiple specular lobes p343.

Anisotropic NDF p343

Note $\theta_m$ Is (polar) angle of the microfacet normal with the macrosurface normal $\mathbf{n}$.

Rough outline:

The tangent and bitangent have to be perturbed by the normal map (and an optional tangent map) to obtain the TBN frame where $\mathbf{m}$ is expressed. p344
Obtain an anisotropic version of the NDF, presented for Beckmann NDF and GGX NDF p345
Optionally use a custom parameterization for both roughness $\alpha_x$ and $\alpha_y$. Presented for Disney principled shading model and Imageworks.

Multiple-bounce surface reflection

Imageworks combines elements from previous work to create a multiple-bounce specular term that can be added to the specular BRDF. $f_{\text{ms}}(\mathbf{l}, \mathbf{v}) = \frac { \overline{F} \text{ } \overline{R_{\text{sF1}}} } { \pi (1 - \overline{R_{\text{sF1}}}) (1 - \overline{F} (1 - \overline{R_{\text{sF1}}})) } (1 - R_{\text{sF1}}(\mathbf{l})) (1 - R_{\text{sF1}}(\mathbf{v}))$

$R_{\text{sF1}}$ is the directional albedo of $f_{\text{sF1}}$
- $f_{\text{sF1}}$ is the specular BRDF term with $F_0$ set to 1
- $R_{\text{sF1}}$ depends on $\alpha$ and $\theta$, it can be precomputed numerically (32x32 texture is enough according to Imageworks).
$\overline{F}$ and $\overline{R_{\text{sF1}}}$ are the cosine weighted averages over the hemisphere.
- $\overline{F}$ closed forms are provided p346
- $\overline{R_{\text{sF1}}}$ can be precomputed in a 1D texture (or curve-fitted), it solely depends on $\alpha$, see p346

BRDF models for subsurface scattering p347

Scoped to local subsurface scattering (diffuse surface response in opaque dielectrics)

Subsurface albedo $\rho_\text{ss}$ is the ratio of energy (of light) that escape a surface compared to the energy entering the interior of the material. It is modeled as an RGB value (a spectral distribution), and often referred as the diffuse color of the surface (Similarly $F_0$ is often referred as the specular color of the surface). It seems it might also be referred as the diffuse reflectance, p450. It is related to the scattering albedo (chapter 14)

For dielectrics, it is usually brighter than the specular color $F_0$. Subsurface albedo results from a different physical process (absorption in the interior, I guess what escape is the complement) than specular color (Fresnel reflectance at the surface). Thus it typically has a different spectral distribution than $F_0$.

Important: Not all values in the sRGB color gamut are plausible subsurface albedos, p349.

Some BRDF models for local subsurface scattering take roughness into account by using a diffuse micro-BRDF $f_\mu$ (microfacet theory), some do not:

If microgeometry irregularities are larger than subsurface scattering distances, microgeometry-related effects such as retroreflection occur.
- A rough-surface diffuse model is used, typically treating ss as local to each microfacet, thus only affecting the micro-BRDF $f_\mu$.
If scattering distances are larger than microgeometry irregularities, the surface should be considered flat when modeling subsurface scattering (retroreflection does not occur). Subsurface scattering is not local to a microfacet, thus cannot be modeled via microfacet theory.
- A smooth-surface diffuse model should be used.

Smooth-surface subsurface models p350

Diffuse shading is not directly affected by roughness.

local subsurface scattering is often modelled with a Lambertian term: $f_\text{diff}(\mathbf{l}, \mathbf{v}) = \frac{\rho_\text{ss}}{\pi}$
It can be improved by an energy trade-off with the surface (specular) reflectance:
- If the specular term is a microfacet BRDF term: $f_\text{diff}(\mathbf{l}, \mathbf{v}) = (1 - F(\mathbf{h}, \mathbf{l})) \frac{\rho_\text{ss}}{\pi} \qquad \text{(9.63)}$
- If the specular term is a flat mirror: $f_\text{diff}(\mathbf{l}, \mathbf{v}) = (1 - F(\mathbf{n}, \mathbf{l})) \frac{\rho_\text{ss}}{\pi} \qquad \text{(9.62)}$

Note: The flat mirror using $F(\mathbf{n}, \mathbf{l})$ and the microfacet specular term using $F(\mathbf{h}, \mathbf{l})$. This is consistent with the fact that for microfacet BRDF, we had set $m = h$.

See section for a larger selection of available equations.

Rough-surface subsurface models p353

Disney diffuse model p353
- by default, use the same roughness as the specular BRDF, which limits materials. But a separate “diffuse roughnes” could be easily added
- Apparently not derived from microfacet theory
Oren-Nayar BRDF (the most-well known) p354
- Assume a microsurface with quite different NDF and masking-shadowing than those used in current specular models.
Derivations from the isotropic GGX NDF:
- Gotanda p355. Does not account for interreflections, has a complex fitted-function.
- Hammon p355. Uses interreflections, fairly simple fitted-function.
  - Fundamentally assumes that irregularities are larger than scattering distances, which may limit materials it can model.

Cloth p356

Wave optics BRDF models p359

Wave optics, or physical optics, by opposition to geometrical optics, is required to model the interaction of light with nanogeometry: irregularities in the range [1-100] wavelength.

No diffraction occurs below 1 wavelength, and above 100 the angle between diffracted light and specularly reflected is so small it becomes negligible.

Diffraction models p360

Nanogeometry causes diffraction.

TODO: define diffraction.

Thin-film interference p361

Thin-film interference is a wave optics phenomenon occuring when light paths reflect from the top and bottom of a thin dielectric layer and interfere with each other. The path has to be short (so the film has to be thin) because of coherence length: the maximum distance a copy of a light wave can be displaced and still interfere coherently (this length is inversely proportional to the bandwidth of the light). For the human visual system (400-700 nm), coherence length is about 1μm.

Layered material p363

Simple and visually significant case of layering is clear coat: a smooth transparent layer over a substrate of a different material.

Visual effect of clear-coat:

Double reflection (clear-coat and underlying substrate). Most notable when the difference in IOR is large (e.g. metal substrate).
Might be tinted (by absorption in the dielectric)
In the general case, layers could have different surface normals (but uncommon for real-time rendering).

Blending and filtering materials p365

Ideally, when blending between materials (when staking, or at mask soft-boundaries), the corect approach would be to compute each material, then blend linearly between them. The same result is achieved by blending the linear parameters and computing the material, but blending non-linear BRDF parameters is theoretically unsound. Yet, in real-time rendering, this is the usual approach, and the results are satisfying.

Blending normal-maps requires special consideration (e.g. treating as a blend between equivalent height-maps), see p366.

“Material filtering is a topic closely related to material blending.” TODO: understand why

specular antialiasing techniques mitigate flickering highlights due to specular aliasing. (e.g. due to linearly filtering normals, or BRDF roughness, which have an non-linear relationship to the final color). There are other potential artifacts (e.g. unexpected changes in gloss with viewer distance), but specular aliasing is usually the most noticeable issue.

Filtering normals and normal distributions p367

Illustrate the issue of naive linear filtering of normal map and roughness.

Propose some solution for better filtering.

Toksvig’s method (intended for Blinn-Phong NDF, but usable with Beckmann): $\alpha_p' = \frac { ||\overline{\mathbf{n}}|| \alpha_p } { ||\overline{\mathbf{n}}|| + \alpha_p (1 - ||\overline{\mathbf{n}}||) }$
- Usable with GGX with translation function for roughness, even though it does not have good theoretical foundation for it.
- Works with the simplest normal mipmapping scheme: linear averaging without normalization.
- Does not work well with compression techniques for normal, which require normals being unit length.

There is another family of mapping techniques (based on mapping the covariance matrix of the normal distribution): LEAN, CLEAN, LEADR. p370 (I do not understant it atm).

TODO: understand what are the variance mapping techniques. variance mapping family of techniques is commonly used for static normal-maps predominent in real-time rendering.

Chapter 10 - Local Illumination p375

There are two solid angles to correctly apply reflectance equation to shade a pixel:

solid angle covered by the pixel projection on the surface. (Addressed in chapter 9, see note below.)
solid angle sustaining all radiance from a light.

Note: figure 10.2 states that chapter 9 presented the integral over the projected footprint of the pixel on the surface. I suppose this is notably because the different texture maps (normal, roughness, …) should ideally represent the averaged value over the fragment surface (especially approaching 1:1 fragment to texel). And the NDF averages the microscale effect at the scale of a fragment.

This chapter aims to take extend shading with the solid angle subtended by actual lights (i.e. not punctual).

10.1 Area Light Source p377

An area light source brightness is represented by its radiance $L_l$.
It subtends a solid angle $\omega_l$ of the hemisphere $\Omega$ of possible incoming light directions around surface normal $\mathbf{n}$.
The area light contribution to the outgoing radiance in direction $\mathbf{v}$ is given by the reflectance equation (presented with the fundamental approximation behind infinitesimal light source) : $L_o(\mathbf{v}) = \int_{l \in \omega_l} f(\mathbf{l}, \mathbf{v}) L_l (\mathbf{n} \cdot \mathbf{l})^+ d\mathbf{l} \approx \pi f(\mathbf{l_c}, \mathbf{v}) \mathbf{c}_\text{light} (\mathbf{n} \cdot \mathbf{l_c})^+ \qquad \text{(10.1)}$

Punctual and directional lights are approximations, thus introducing visual errors depending on two factors:

size of the light source (measured as the solid angle it covers from the shaded point). Smaller is less error.
glossiness of the surface. Rougher is less error.

Observations:

For a given difference in subtended angle, rougher surface show less size difference in resulting specular highlight.
The rougher the surfaces, the larger the specular highlight

Lambertian surfaces

For Lambertian surface, area light can be computed exactly using a point light. For such surfaces, outgoing radiance is proportional to the irradience $E$ (TODO: why?): $L_o(\mathbf{v}) = \frac{\rho_\text{ss}}{\pi}E \qquad \text{(10.2)}$

vector irradiance (initially introduced as light vector) $\mathbf{e}(\mathbf{p})$ allows to convert an area light source (or several) into a point or directional light source. $\mathbf{e}(\mathbf{p}) = \int_{\mathbf{l} \in \Theta} L_i(\mathbf{p}, \mathbf{l}) \mathbf{l} d\mathbf{l} \qquad \text{(10.4)}$ (where $\Theta$ is the whole sphere)

IMPORTANT: following derivations are correct only if there is no “negative side” irrandiance.

The general solution is then to use the substitutions: $\mathbf{l}_c = \frac{\mathbf{e}(\mathbf{p})}{|| \mathbf{e}(\mathbf{p}) ||}$ $\mathbf{c}_\text{light} = \mathbf{c}' \frac{|| \mathbf{e}(\mathbf{p}) ||}{\pi} \qquad \text{(10.7)}$

TODO: I did not understand the derivation in this section

Special case of spherical light

For a spherical light source centered at $\mathbf{p}_l$ with radius $r_l$. It emits a constant radiance $L_l$ from every point on the sphere, in all directions:

$\mathbf{l}_c = \frac{\mathbf{p}_l - \mathbf{p}}{|| \mathbf{p}_l - \mathbf{p} ||}$ $\mathbf{c}_\text{light} = \frac{r_l^2}{|| \mathbf{p}_l - \mathbf{p} ||^2} L_l \qquad \text{(10.8)}$

Which is the same as an omni light with $c_{\text{light}_0} = L_l$, $r_0 = r_l$, and a standard inverse square distance falloff.

wrap lighting

wrap lighting seems to mean a lighting that “wraps” the scene. It is achieved in rendering by modifying the usual $\mathbf{n} \cdot \mathbf{l}$ value before clamping it to 0. TODO: get a more rigorous definition

From the observation that effects of area lighting are less noticeable for rough surface : wrap lighting gives a less physically based but effective method to model area lighting of Lambertian surfaces.

\[E = \pi c_\text{light} \left( \frac{(\mathbf{n} \cdot \mathbf{l}) + k_\text{wrap}}{1 + k_\text{wrap}} \right)^+ \qquad \text{(10.9)}\]

with $k_\text{wrap}$ in the range $0$ (point light) to $1$ (area light covering the hemisphere).

Valve form to mimic a large area light:

\[E = \pi c_\text{light} \left( \frac{(\mathbf{n} \cdot \mathbf{l}) + 1}{2} \right)^2 \qquad \text{(10.10)}\]

10.1.1 Glossy Materials p382

Model the effect of area lights on non-Lambertian materials:

Primary effect is the highlight, with size and shape similar to the area light (edge blurred according to roughness)

Usual methods (which is used in real-time rendering for a variety of problems) are based on finding, per shaded point, an equivalent punctual light setup that would mimic the effect of non-infinitesimal light.

Mittring’s roughness modifification p383 alters roughness parameter to reshape the BRDF specular lobe.
- Karis applies it to GGX BRDF and spherical area light: $\alpha' = \left( \alpha_g + \frac{r_l}{ 2 || \mathbf{p}_l - \mathbf{p} || } \right)^\mp$
  - breaks for very shiny materials.
most representative point solution p384 represent area lights with a light direction that changes with the point being shaded: the light vector is set to the direction of the point on the area light contributing the most energy toward the surface.
- Note: This ressemble the idea of importance sampling in Monte Carlo integration (numerically computing a definite integral by averaging samples over the integration domain).
  - importance sampling: prioritize samples with a large contribution to the overall average, which is a variance reduction technique.
  - Monte Carlo integration is based on sequence of pseudo-random numbers
  - Quasi-Monte Carlo, by contrast use low-discrepency sequences (also called quasi-random sequences)

10.1.2 General Light Shapes p 386

tube lights or capsules p387
planar area lights p388 are defined as a section of a plane bound by a geometrical shape:
- card light are bound by rectangle
  - Drobot developed one of the first practical approximations p388 (a representative point solution)
- disk lights are bound by a disk
- polygonal area lights are bound by a polygon
  - Lambert, refined by Arvo then Lecocq, for glossy materials modeled as Phong specular lobes p389

A different approach is linearly transformed cosines (LTCs) p390 is practical, accurate and general (more expensive that representative point, but much more accurate).
Cosines on the sphere are expressive (via linear transformation) and can be integrated easily over arbitrary spherical polygon. The key observation is that integration of the LTC (with 3x3 transform $T$) over a domain is equal to the integral of the cosine lobe over the domain transformed by $T^{-1}$.

Approximations have to be found to express generic BRDFs as one or more LTCs over the sphere.

10.2 Environment Lighting p391

Although there is not physical difference, in practice implementations distinguish between:

direct light usually with relatively small solid angle and high radiance (should cast shadows).
indirect light tends to diffusely cover the the whole hemisphere, with moderate to low radiance.

Note: This section talks about indirect and environment lighting, but does not investigate global illumination. The distinction is that the shading does not depend on the other surfaces in the scene, but rather on a small set of light primitives. (i.e. the shading algorithm receives light sources as input, not other geometry).

Ambient light

Simplest model of environment lighting is ambient light: the radiance does not vary with direction, it has constant value $L_A$.

For arbitrary BRDF, the integral is the same as the directional albedo $R(\mathbf{v})$: $L_o(\mathbf{v}) = L_A \int_{\mathbf{l} \in \Omega}{f(\mathbf{l}, \mathbf{v}) (\mathbf{n} \cdot \mathbf{l}) d\mathbf{l}} = L_A R(\mathbf{v})$

And for the particual case of Lambertian surfaces: $L_o(\mathbf{v}) = \frac{\rho_\text{ss}}{\pi} L_A \int_{\mathbf{l} \in \Omega}{(\mathbf{n} \cdot \mathbf{l}) d\mathbf{l}} = \rho_\text{ss} L_A$

10.3 Spherical and Hemispherical Functions p392

To extend environment lighting beyond a constant term, incoming radiance should depend on direction onto the object. This can be represented by spherical functions: defined over the surface of the unit sphere, or over the space of direction in $\mathbb{R}^3$. This domain is denoted $S$.

spherical bases are the representations, presented later TODO: define much better

projection is converting a function to a given representation.
reconstruction is evaluating the value of a fuction from a given representation.

10.3.1 Simple Tabulated Forms

Representation is a table of values associated to a selection of several directions. Evaluation involves finding a number of samples around the evaluation direction and reconstructing the value with some interpolation.

Ambient cube (AC) is one of the simplest tabulated forms p395. It is equivalent to a cube map with a single texel on each cube face.

10.3.2 Spherical Bases p395

Spherical radial basis functions (SRBF) p396:

Spherical Gaussians (SG) (or von Mises-Fisher distribution in directional statistics) p397
- One drawback is their global support: each lobe is non-zero for the entire sphere. Thus if N lobes are used to represent a function, all N lobes are needed for reconstruction.
Spherical harmonics (SH) p398 (more rigorously: real spherical harmonics, only the real-part)
Linearly Transformed Cosines (LTC) representation can efficiently approximate BRDFs.
Spherical wavelets p402 basis balances locality in space (compact support) and in frequency (smoothness).
Spherical piecewise constant basis functions
Biclustering approximations

10.3.3 Hemispherical Bases p402

For hemispherical functions, half of the signal is zero, hemispherical bases are less wasteful. This is especially relevant for functions defined over surfaces (BRDF, incoming radiance, irradiance arriving at a point).

Ambient/Highlight/Direction (AHD) basis p402 TODO: understand
Radiosity normal mapping (or Half-Life 2 basis) p402 TODO: understand
- works well for directional irradiance
Hemispherical harmonics (HSHs), specialize spherical harmonics to the hemispherical domain.
- H-basis take part of the SH basis for longitudinal parameterization and parts of the HSH for latitudinal.
  - Allows for efficient evaluation

10.4 Environment Mapping p404

Environment mapping: records a spherical function in one or more images. (Typically uses texture mapping to implement lookups in the table).

This is a powerful and popular form of environment lighting.
Trades a large memory usage for simple and fast decode.
Highly expressive:
- higher frequency by increasing resolution
- higher range of radiances by increasing bit depth of channels

A limitation of environment mapping: it does not work well with large flat surfaces. They will result in a small part of the environment table mapped onto a large surface.

Image-based lighting (IBL) p406 is another name for illuminating a scene with texture data, typically when the environment map is obtained from real-world HDR 360° panoramic photographs.

Shading techniques make approximations and assumptions on the BRDF to perform the integration of the environment lighting:

reflection mapping: most basic case of environment mapping, assuming the BRDF is a perfect mirror.
- An optically flat surface, or mirror, reflects an incoming ray of light to the light’s reflection direction $\mathbf{r}_i$. Outgoing radiance includes incoming radiance from just one direction (reflected view vector $\mathbf{r}$).
- Reflectance equation for mirrors is greatly simplified: $L_o(\mathbf{v}) = F(\mathbf{n}, \mathbf{r}) L_i(\mathbf{r}) \qquad \text{(10.29)}$
  - $L_i$ only depends on the direction, it can be stored in a two-dimensionnal table (the textures), called an environment map.
  - Access information is computed by using some projector function: maps $r$ into one or more textures.

A variety of projector functions:

Latitude-longitude mapping (or lat-long mapping) p406
- Keeps distance between latitude lines constant, unlike Mercator projection
Sphere mapping p408
- Texture image is derived from the environment viewed orthographically in a perflectly reflective sphere: the circular texture is called a sphere map or light probe (it captures the lighting situation at the sphere’s location) .
  - Photographs of spherical probes is an efficient method to capture image-based lighting.
- Drawback is that the sphere map captures a view of the environment only valid for a single view direction.
  - Conversion to other view directions is possible, but can result in artifacts due to magnification and singularity around the edge.
- The reflectance equation can be solved for an arbitrary isotropic BRDF and results stored in a sphere map.
  - This BRDF migh include diffuse, specular, retroreflection, and other terms.
- Several sphere maps might be indexed, e.g. one with reflection vector, one with surface normal to simulate specular and diffuse environment effects.
Cube mapping p410
- Most popular tabular representation for environment lighting, implemented in hardware by most modern GPUs.
- Accesses a cube map (originally cubic environment map), created by projecting environment onto the sides of a cube.
- view-independent (unlike sphere mapping) and has more uniform sampling that lat-long mapping.
  - isocube mapping p412 has even lower sampling-rate discrepencies while using same hardware.
Dual paraboloid environment mapping p413
Octahedral mapping p413 maps the surrounding sphere to an octahedron (instead of a cube)
- good alternative when cube map texture hardware is not present
- can also be used as compression method to express 3D directions (normalized vectors) using 2 coordinates.

10.5 Specular Image-Based Lighting p414

Extension of environment mapping, originally developed for rendering mirror-like surfaces, to glossy reflections.
The environment map also called specular light probe when used to simulate general specular effects for infinitely distant light sources

Note: probing term is used because the map captures the radiance from all directions at a given point in the scene.

specular cube maps is used for the common case of storing in cube maps.

TODO: p423 fig. 10.38 understand why the GGX BRDF lobe, in red, is stronger when the polar coordinate is larger than this of the reflection vector. I would expect it to be the other way, as masking-shadowing should be larger as incoming light gets further away from the surface normal and $\mathbf{n} \cdot \mathbf{l}$ gets smaller (which seems to be consistent with the “off-specular” figure 11 of mftpbr).

10.6 Irradiance Environment Mapping p424

Categorization:

Environment maps for specular reflections:
- Indexed by the reflection direction (potentially skewed).
- Contain radiance values.
- Unfiltered: used for mirror reflections.
  - Contain incoming radiance values, along the sampled direction.
- Filtered: used for glossy reflections.
  - Contain outgoing radiances values, along the view vector reflecting the sampled direction.
Environment maps for diffuses reflections:
- Indexed by the surface normal.
- Contain irradiance values.

Other representations

Precomputed radiance transport (PRT) is the general idea of precomputing lighting to account for all interactions.

10.7 Sources of Error

A common real-time engine approach:

Model a few important lights analytically. Approximate integrals over light area and compute shadow maps for occlusion
Other light sources (distant, sky, fill, light bounces over surfaces) are represented:
- by environment cube maps for the specular component
- by spherical bases for diffuse irradiance

In such mix of technique, the consistency between different forms of lighting might be more important than absolute error committed by each.

Chapter 11 Global Illumniation - p437

Radiance is the final quantity computed by the rendering process. So far we used the reflectance equation.

11.1 The Rendering Equation p437

The full rendering equation was presented by Kajiya in 1986. We use the following form:

\[L_o(\mathbf{p}, \mathbf{v}) = L_e(\mathbf{p}, \mathbf{v}) + \int_{\mathbf{l} \in \Omega}{ f(\mathbf{l}, \mathbf{v}) L_o(r(\mathbf{p}, \mathbf{l}), -\mathbf{l}) (\mathbf{n} \cdot \mathbf{l})^+ d\mathbf{l}} \qquad\text{(11.2)}\]

With the following differences from the reflectance equation:

$L_e(\mathbf{p}, \mathbf{v})$ is the emitted radiance from location $\mathbf{p}$ in direction $\mathbf{v}$.
$L_o(r(\mathbf{p}, \mathbf{l}), -\mathbf{l})$ (replacing $L_i(\mathbf{p}, \mathbf{l})$) states that incoming radiance at $\mathbf{p}$ from $\mathbf{l}$ is equal to the outgoing radiance from another point defined by $r(\mathbf{p}, \mathbf{l})$ in the opposite direction $-\mathbf{l}$.
- $r(\mathbf{p}, \mathbf{l})$ is the ray casting function, it returns the location of the first surface point hit by a ray cast from $\mathbf{p}$ along direction $\mathbf{l}$.

Defining $L_o$ in term of the integration of other $L_o$ makes it a recursive integral.

Important properties of the rendering equation:

It is linear with respecte to the emitted lighting (scaling the light sources scale the result by same factor).
The response for each light is independent from all other sources (thus each could be computed in isolation).

The local lighting model need the surface data only at visible points to compute the lighting. (Common in real-time rendering, being what GPUs are most efficient: processing primitives independently).

Transparency, reflections, shadows are thus example of global illuminations algorithms (using information from other surfaces than the point currently illuminated).

Alternatively, in local lighting model, photons travel from the light to a surface (illuminated point) then to the eye. Above global illuminations effects consider interaction of photons with other intervening objects:

Shadowing consider intervening objects’ direct occlusion
Reflections can use environment or irradiance map to capture light reaching distant objects and reflect it to compute the illumination of local surfaces.

Heckbert developed a notational scheme to formally describe the paths simulated by a technique:

$L$: light
$E$: eye
$D$: diffuse photon interaction
$S$: specular photon interaction

Note: Categorization can be extended. Defines “glossy” as: shiny but not mirror-like (p439).

Algorithms are briefly summarized via regular expressions describing what interaction they simulate. e.g.:

Direct illumination: $L(D S)E$. If light have a geometry and go directly to the eye: $L(D S)?E$.
Environment mapping: $L(D (S D)?S)E$
The rendering equation: $L(D S)*E$.

Global illumination research focuses on methods to compute light transport along some of these paths.Two common strategies are to simplify and to precompute.

TODO: define light transport

11.2 General Global Illumination p441

Algorithms to solve the fulle rendering equation: instead of incoming radiance $L_i$ being given, radiance is emitted or reflected from other points.

11.2.1 Radiosity p442

Radiosity was the first CG technique to simulate bouched light between diffuse surfaces: $LD*E$. It can compute interreflections ans soft shadows. The name comes from the quantity that is computed by the algorithm.

It relies on the finite element method and consider each surface a light source at equilibrium.

Radiosity see each surface as composed of some patches, each with an average radiosity value. The radiosity for patch $i$ is: $B_i = B^e_i + \rho_{ss} \sum_j{F_{ij} B_j} \qquad\text{(11.4)}$

$B^e_i$ is the radiant exitance of patch $i$ (the radiosity it emits). Non-zero only for light sources.
$\rho_{ss}$ is the subsurface albodo.
$F_{ij}$ is the form factor between patches $i$ and $j$, a geometric term giving the fraction of uniform diffuse randiant energy leaving patch $i$ that is incident upon patch $j$. These fractions add up to $1$: (TODO: are patch indices reversed? We copied the book)
- \[F_{ij} = \frac{1}{A_i} \int_{A_i}{ \int_{A_j}{ V(\mathbf{i}, \mathbf{j}) \frac{\cos{\theta_i} \cos{\theta_j}}{\pi d^2_{ij}} da_i da_j } } \qquad\text{(11.5)}\]
  - $A_i$, $A_j$: the areas of patches $i$ and $j$.
  - $V(\mathbf{i}, \mathbf{j})$: the visibility function between points $i$ and $j$ ($0$ if occluded, $1$ otherwise).
  - $\theta_i$, $\theta_j$: angle between the patch normal and the ray connecting points $i$ and $j$.
  - $d_{ij}$: length of the ray (distance between points $i$ and $j$).

Equations (11.4) for all patches are combined in a single linear system that is then solved to obtain the radiosity value for every patch.

Ray Tracing 11.2.2

ray casting is the process of firing a ray from a location to determine what objects are in a particular direction (i.e. visibility?)
ray tracing uses rays to determine light transport between scene elements.

Classical ray tracing / most basic form: shot rays from camera through pixel grid. From the closest hit, shoot rays toward light (determine shadow or transparent attenuation/refraction), in reflected or refracted direction, as approriate. It is limited to hard shadows, sharp reflections and refractions. Is it what is called a Whitted raytracer? (from Turner Whitted).

This underlying principle can be used to solve the full rendering equation $L(D|S)*E$. Shooting rays and evaluating how much light they carry is used to compute the integral in (11.2). Because of the recursion, for every ray the integral is evaluated again at the intersection. Integrals are evaluated via Monte Carlo methods.

Ray are shot to point-sample the integrand. At the intersection, the new integral is solved by point-sampling the integral again. The ray bounces to build a path, the light carried along each path provides one evaluation the integrand: this procedure is called path tracing.

Path tracing can render mirror-like, glossy or diffuse material, soft shadows, transparent objects along with caustic effects. It can handle fog and subsurface scattering if extended to sample points in volumes.

Downside is computational complexity, and high variance (close points could have vastly different lighting) which manifests as noise. importance sampling can be used to mitigate this effect without additional paths.

11.3 11.4 are concerned with occlusions (visibility of light sources from shaded points). 11.5 11.6 are simulating not only occlusion bu also full light bounces.

11.3 Ambient Occlusion p446

Ambient occlusion (AO) is a basic global illumination effect developped in early 2000s. It inexpensively provides cues about shapes when lightin lacks directional variations (e.g. environment lighting).

11.3.1 Ambien Occlusion Theory p446

Surface irradiance is the cosine-weighted integral of incoming radiance, assumed constant here $L_i(\mathbf{l}) = L_A$: $E(\mathbf{p}, \mathbf{n}) = \int_{\mathbf{l} \in \Omega}{L_A (\mathbf{n} \cdot \mathbf{l})^+ d\mathbf{l}} = \pi L_A \qquad\text{(11.6)}$

For Lambertian surfaces, outgoing radiance $L_o$ is proportional to surface irradiance $E$. From (11.6), it results that $L_o$ is constant under constant uniform illumination, as it does not depend from location $\mathbf{p}$ or normal $\mathbf{n}$. It leads to a flat appearance.

It can be extended with visibility $v(\mathbf{p}, \mathbf{l})$ that equals $0$ if a ray cast from $\mathbf{p}$ in direction of $\mathbf{l}$ is blocked, $1$ otherwise: $E(\mathbf{p}, \mathbf{n}) = L_A \int_{\mathbf{l} \in \Omega}{v(\mathbf{p}, \mathbf{l}) (\mathbf{n} \cdot \mathbf{l})^+ d\mathbf{l}} \qquad\text{(11.7)}$

Ambient occlusion $k_A(\mathbf{p})$ is the cosine-weighted integral of the visibility function, a cosine-weighted percentage of the unoccluded hemisphere: $k_A(\mathbf{p}) = \frac{1}{\pi} \int_{\mathbf{l} \in \Omega}{v(\mathbf{p}, \mathbf{l}) (\mathbf{n} \cdot \mathbf{l})^+ d\mathbf{l}} \qquad\text{(11.8)}$

Giving: $E(\mathbf{p}, \mathbf{n}) = k_A(\mathbf{p}) \pi L_A \qquad\text{(11.9)}$

This way, irradiance changes with surface location $\mathbf{p}$.

The bent normal is the cosine-weighted average unoccluded direction: $n_{bent} = \frac {\int_{\mathbf{l} \in \Omega}{\mathbf{l} v(\mathbf{l}) (\mathbf{n} \cdot \mathbf{l})^+ d\mathbf{l}}} {|| \int_{\mathbf{l} \in \Omega}{\mathbf{l} v(\mathbf{l}) (\mathbf{n} \cdot \mathbf{l})^+ d\mathbf{l}} ||} \qquad\text{(11.10)}$

11.3.2 Visibility and Obscurance p449

Obscurance modifies the ambient occlusion computation, to replace visibility function $v(\mathbf{l})$ with a continuous distance mapping function $\rho(\mathbf{l})$ (valued $1$ above $d_{\text{max}}$): $k_A(\mathbf{p}) = \frac{1}{\pi} \int_{\mathbf{l} \in \Omega}{\rho(\mathbf{l}) (\mathbf{n} \cdot \mathbf{l})^+ d\mathbf{l}} \qquad\text{(11.11)}$

11.3.3 Accounting for interreflections p450

Reasoning to assume that $L_i$ from blocked directions is equal to $L_o$ of currently shaded point, to obtain a new factor $k’_A$: $k'_A = \frac{k_A}{1 - \rho_{ss}(1 - k_A)} \qquad\text{(11.13)}$

11.3.4 Precomputed Ambient Occlusion p451

The process of precomputing any lighting-related information is often called baking.

Malley’s method use importance sampling, casting a cosine-weighted distribution of ray, to compute AO.

Pointers to precompute data to model AO effects of objects on each other p452. Pointers to use AO in indirect illumination solutions p453.

Note: AO decouples visibility calculations from lighting (so, usable with dynamic lighting).

11.3.5 Dynamic Computation of Ambient Occlusion p453

Provide better results for dynamic scenes. Two groups of methos:

Object space
- Disk at vertices, SDF, cone tracing p455, collection of spheres with SH p456
  - SH methods producing high-order coefficients augment AO with directional occlusion info
Screen space

11.3.6 Screen-Space Methods p457

Screen-space ambient occlusion (SSAO) is a dynamic method developed by Crytek compute AO in a full-screen pass using z-buffer only. Also points at other methods with ad-hoc heuristics.

SSAO could be interpreted as Monte Carlo integration, calculating the volumetric obscurance $v_A$ p459 (11.15).

It can be augmented with normal buffer, e.g. volumetric ambient occlusion p459.

Horizon-base ambient occlusion (HBAO) estimate visibility by determining horizon angles. Ground-truth ambient occlusion (GTAO) is an horizon-based approach aiming to match results from ray tracing.

To limit the required number of samples, screen-space methods employ some form of spatial-dithering (TODO: define in this context.), such as using slightly different set of samples, followed by full-screen joint bilateral filtering. Calculations can also be supersampled over time, requiring previous data to be reprojected to current view.

11.3.7 Shading with Ambient Occlusion p463

Apply AO to more complex lighting scenarios, lifting the limitation to constant illumination. Demonstration to arrive at: $L_o = k_A \rho_{ss} \int_{\mathbf{l} \in \Omega}{L_i(\mathbf{l}) K(\mathbf{n}, \mathbf{l})d\mathbf{l}} \qquad\text{(11.22)}$

With: $K(\mathbf{n}, \mathbf{l}) = \frac {v(\mathbf{l}) (\mathbf{n} \cdot \mathbf{l})^+} {\int_{\mathbf{l} \in \Omega}{v(\mathbf{l}) (\mathbf{n} \cdot \mathbf{l})^+} d\mathbf{l}} \qquad\text{(11.23)}$

(11.22) can be thought as applying filter $K$ to incoming radiance $L_i$.

On appraoch it to approximate $K$ with a simpler filter, such as the normalized cosine kernel $H$: $H(\mathbf{n}, \mathbf{l}) = \frac {(\mathbf{n} \cdot \mathbf{l})^+} {\int_{\mathbf{l} \in \Omega}{(\mathbf{n} \cdot \mathbf{l})^+} d\mathbf{l}} \qquad\text{(11.24)}$

This approximation gives: $L_o = \frac{k_A}{\pi} \rho_{ss} E \qquad\text{(11.25)}$

This means that, in this simple form, shading with AO can by performed by computing irradiance (e.g. irradiance env map) and multiplying it by AO value $k_A$.

Note: Ignoring visibility, as in (11.25), is a significant approximation. This approximation highlights why AO is not a good choice for modeling visibility of highly directional lights (it entirely remove light visibility from the equation).

Also, we assumed Lambertian surfaces, as a more complex non-constant BRDF cannot be pulled out of the integral. So AO makes most sense for diffuse BRDFs.

Using the bent normal make for a better approximation of (11.23), p 467.

11.4 Directional Occlusion p467

AO is a poor approximation for visibility for lights with more directionality (area light, punctual, …) or complexity (e.g. strong gradient), and cannot correctly deal with glossy BRDFs.

This section will focus on methods that the entire spherical or hemispherical visibility. Meant to be used mainly for occlusion of large area light or environment lighting, where generated shadow are soft (and artifacts caused by approximated visibility are not noticeable). Alternatively, can provide occlusion when regular shadowing techniques are not feasible (self-shadowing bump-map, extremely large scene).

11.4.1 Precomputed Directional Occlusion p 466

ambient aperture lighting models the set of unoccluded 3D directions as a whole as an circular aperture. (Other methods could use elliptical aperture).

Possibility to use spherical signed distance function (SSDF) to represent visibility. Or any spherical/hemispherical base can encode visibility.

As with AO, directional visibility information can be stored in textures, mesh vertices, or volumes.

11.4.2 Dynamic Computation of Directional Occlusion p467

Note: Using more bands in SH allow encoding visibility with more precision.

Many methods used in AO can be used to generate directional visibility information. Cone tracing can be restricted to one direction. Also screen-space methods, e.g. screen-space bent cones.

11.4.3 Shading with Directional Occlusion p468

Visibility function is $0$ when light:

falls under the horizon (horizon mapping)
falls outside the visibility cone (ambient aperture lighting)
falls in the negative area of the SSDF

Distinct approximations and restrictions, offering trade-offs between generality, runtime cost and quality.

Present reasoning for punctual lights p468, extend to area-lights p468 (visibility is $0$ except in a solid angle subtended by the light), assuming Lambertian surface (i.e. constant BRDF).

Move onto environment lighting (remove restriction on solid angle), still Lambertian p470
Introduce zonal harmonics (ZH), a subset of SH for which a single coefficient per band is non-zero. The cosine $\mathbf{n} \cdot \mathbf{l}$ projects to ZH.
Precomputing $\bar{v(\mathbf{l})} = v(\mathbf{l})(\mathbf{n} \cdot \mathbf{l})^+$ is a form of precomputed radiance transfer. It prevents fine-scale modification of the normal.

Then onto glossy BRDFs (not constant), with or without dependence on view angle p471.
Can approximate the BRDF with a set of spherical Gaussians, representable by:

direction (or mean) $d$, standard deviation $\mu$, amplitude $w$.

11.5 Diffuse Global Illumination

Cover simulating full light bounce in real time, last bounce of a diffuse surface, i.e light path: $L(D|S)*DE$. Assume lighting changes smoothly (or is constant) on hemisphere above shaded point.

11.5.1 Surface Prelighting p473

Precompute the results of expensive computation for static objects, as baking prevents changing geometry, lights or materials. Dynamic objects act only as receivers (they neither occlude light nor generate indirect illumination): their effect is either ignored or modeled with other techniques (e.g. screen-space occlusion).

Simplest lighting info to precompute is irradiance. Light source independence allows to add dynamic lights on top of precomputed irradiance. Exitance is irradiance times diffuse color. Since diffuse color is high-frequency but repeatable, while irradiance is low-frequency but unique, it is better to store them separated.

TODO: why irradiance can only be precomputed for flat-surfaces? What prevents a statically known but spatially varying normal?

11.5.2 Directional Surface Prelighting p475

Prelighting together with normal mapping on Lambertian surfaces. Also coverage of dynamic geometry.

General method is storing full spherical irradiance, e.g. in SH

3rd order (9 coeff) give excellent results but storage & bandwith costs are high.
2n order (4 coeff) is less costly, but the quality is visibly degraded. Present variations, both for lower cost or high quality.

TODO: For a high quality approach also usable for low-gloss specular BRDF see: Pettineo, Matt, “SG Series Part 6: Step into the Baking Lab,” The Danger Zone blog, Oct. 9, 2016.

11.5.3 Precomputed Transfer p 478

Precomputed lighting is inherently static. It is possible to precompute how light interacts with (static) models and allow light to change (at runtime cost).

Function that take incoming lighting and return a descrption of the radiance distribution throughout the scene is called transfer function. Solutions that precompute this are called precomputed transfer or precomputed radiance transfer (PRT).

Techniques to precompute transfer from a number of elements then used to model the lights

e.g. Precompute how the scene respond to light distribution represented by SH basis functions. Then project a dynamic environment lighting to those SH bands. p480.

Discussion of applying principal component analysis (PCA) p480.

Applying to indoor lighting with clustered static lights then interpolated for the dynamic lighting p481.

Techniques to precompute transfer between surfaces p482

TODO: understand

The actual source of illumination becomes irrelevant. Seems to imply we do direct-illumination calculations on “source” elements. TODO: How? There is also a set of “receiver” elements. The preprocessing step computs how light is transferred between sources and receivers.

The outgoing radiance for all source elemnts is provided to the system. TODO: How?

Draws from progressive radiosity as it computes one light bounce at a time (and does not solve a system of linear equations, unlike radiosity). The process of transferring radiance to the receiving location is called gathering.

11.5.4 Storage Methods p484

Note: those methods can also be used to store ambient and directional occlusion, as they share many spatial characteristics of diffuse lighting. p491

When values are filtered on the GPU, care must be taken to obtain valid values (e.g. renormalize).

light maps collectively describe all textures that store precomputed lighting information. More specific terms might be used to denote the specific type of data, such as irradiance map.

Mipmapping usually not needed (a lightmap texel covering a large area of geometry). Since lightmap texels are not reused, mapping require an unique parameterization.

charts or shells are the chunks of mesh in texture space. Charts filtering footprints must stay separate to avoid bleeding. grid-preserving parameterization can be used to create ligtmaps free from seam artifacts.

Storing precomputed lighting on vertices is rarely used p487.

(alternative to light maps) Irradiance volumes represent 5-dimensional irradiance function with sparse spatial sampling of irradiance env maps: it store 2 directional irradiance env map (directional) (TODO: the envmap are also called probes?) on a 3-dimensional (spatial) grid in space. Irradiance function at sample points are commonly: SH, spherical Gaussians, ambient cube, ambient dice. Dynamic objects can interpolate irradiance values from closest maps. Static surfaces can also be lit by irradiance volumes, avoiding the need for parameterization of the light map.

The volumetric structure that holds lighting can be irregular. e.g. Delaunay tetrahedralization p 489.

The position for which lighting gets stored are referred as lighting probes (also, light probes, to distinguish from “light probes”: the distant lighting recorded in an envmap).

Note: algorithm to traverse a tetrahedral mesh to find the tetrahedron for a given absolute position p490, figure 11.31

It is common to use different lighting storage for static (e.g light maps) vs dynamic (e.g. volumetric structures) p490.

11.5.5 Dynamic Diffuse Global Illumination p491

Note: In many case, a single bounce is enought to create believable results.

“Instant Radiosity” place virtual point lights (VPLs), and inspired reflective shadow maps (RSM): The map store more information about surfaces than depth: albedo, normal, direct illumination (flux). Can be optimized by creating some lights from the RSM and splatting them in screen space. Main drawback: no occlusion for indirect illumination.

11.5.6 Light Propagation Volumes p493

Light Propagation Volumes (LPV) is inspired from discrete ordinate methods from radiative transfer theory. It discretizes the scene into a regular grid of 3D cells, and incrementally propagate the directional distribtion of radiance flowing through them. Important advantage: geneates a full radiance field for each cell.

There is a cascaded variant. It is possobile to accout for occlusion of indirect lighting.

Suffer from bleeding, commong to volumetric approaches. And also aliasing.

11.5.7 Voxel-Based Methods p494

Voxel cone tracing global illumination (VXGI) store the geometry in a sparse voxel tree, voxels also contain information of light reflected off their geometry. Then, bundles of rays are approximated by cone tracing. The number of cones traced must be balanced with rendering budget (usually require spatial distribution & filtering).

Sparse octree can stall warps on memory latency (high number of dependent reads, little logic work) Can be mitigated using cascaded 3D texture (no dependent reads).

11.5.8 Screen-Space Methods p496

Screen-space methods for diffuse GI are not as popular as SSAO: artifacts are pronunced (missing information, result highly dependent on viewpoint). Can nonetheless be used to augment some other solution (e.g. irradiance volumes) at fine scale.

11.6 Specular Global Illumination - p497

Cover simulating full light bounce in real time, last bounce of a specular surface, i.e light path: $L(D|S)*SE$. Assume lighting has high rate of change accross incident directions.

Unlike diffuse GI, those methods that can render view-dependent effects. For glossy material, specular lobes are much tighter: radiance representation should deliver high-frequency details, and the reflectance equation only need lighthing incident from a limited solid angle (where Lambiertian BRDF reflect illumination from entire hemisphere).

Method storing incident radiance can deliver crude view-dependent effects. Artifacts can be reduced by representing lighting with higher precision e.g. p498 9 to 12 Gaussian lobes can model moderately glossy materials.

11.6.1 Localized Environment Maps p498

Previous methods could not render polished materials, since the radiance field is too coarse.

The most popular solution to deliver specular component for GI in real-time: localized environment maps p498 trade spatial precision for angular precision. It relies on sparsely distributed refelection probes: environment maps (EM) rendered at specific points in the scene.

Note: perfect reflections are specular indirect illuminations.

Results diverge from reality as rendered specular-surface location gets further from EM center. parallax correction mitigate the problem: simple shapes, reflexion proxies, approximate the environment geometry, and allow to find a much better reflection direction $r’$ to index the EM.

Popular because of many advantages:

Easy to implement, compatible with both forwared and deferred rendering schemes
Fast at runtime
Give direct artistic control over the look and memory usage (via density, placement, surface affinity, blending)
Glossy materials can index mip levels of a prefiltered EM depending on roughness and distance to proxy shape.

Drawbacks:

Proxy shapes mismatch make reflections stretch in unnatural ways
Reflective objects rendered into the EM have their specular BRDF evaluated from the EM location, which diverge from the surface location accessing the EM, so the view of reflected object is not correct.
Light leaks, as simplified ray cast misses local occluding geometry. Can be mitigated:
- directional occlusion methods (section 11.4)
- use diffuse lighting higher spatial resolution: divide the EM value by the average diffuse lighting at the position the EM is rendered, multiply by diffuse lighting at shaded location p502.

Extensions use more sophisticated representation of geometry captured by reflection probles (e.g. depth).

11.6.2 Dynamic Update of Environment Maps - p502

Possiblity to update probes at low frequency (they should react to time of day), while approximating reflections of dynamic geometry (e.g. screen-space methods). If dynamic are rendred in probes, heuristics can still be used for lower frequency.

Optimizations for filtering and BC6H compression p503.

An optimization to avoid expensive scene submission is offline rendering of a G-buffer of the static geometry (then optionally render dynamic objects on top at runtime), and use it to render the cubemap faces.

11.6.3 Voxel-Based Methods

Offer much better spatial precision than localized EMs but require more performance.

Voxel cone tracing (section 11.57) is less expensive for specular case, because a single cone is usually enough for glossy materials (fallback to localized reflection for specular contribution on rougher materials). For very narrow BRDF, if voxelized cubes become apparent, other methods can provide perfect mirror reflections at lower runtime cost.

11.6.4 Planar Reflections p504

Restricted to planes, but work for glossy (with filtering) as well as perfect mirrors Can be achieved by simple modification of the projection matrix, and a programmed clipping plane p505.

11.6.5 Screen-Space methods - p505

Slightly more precise than the diffuse case, the family of methods is called screen-space reflections (SSR).

Overal idea is to find intersection of reflected ray with geometry in z-buffer, and assume Lambertian geometry on hit.

digital differential analyzer (DDA) is an algorithm to interpolate variables between start and end point.

Basic form use a single ray to profile only mirror reflections, but SSR can also render glossy reflections. E.g. importance sampling shooting rays stochastically p507, reuse, filtering spatially and temporally. Sampling can be optimized using a hierarchical depth buffer.

TODO: understand why info about the thickness of objects in depth buffer would be useful p509

SSR is great to provide some effects (e.g. local reflection of nearby objects on mostly flat surfaces), but are not a complete solution. Different methods should be stacked, e.g.:

SSR as first layer
localized reflections probes as fallback
- global default probe for areas whithout local probes

11.7 Unified Approaches p509

A saying of graphics community: “Ray tracing is the technology of the future and it always will be!”. It implies that there will always be more efficient ways to handle particular parts of the rendering pipelines (e.g. primary visibility).

A more reasonable / less pure approach is to use path-tracing for effects difficult with rasterization. e.g.:

Trace paths for reflexion instead of approximate reflection proxies / incomplete scree-space info.
Trace rays toward area lights to compute occlusion instead of shadows with ad hoc blurs.

Real-time rendering has always been about compromises (such as composition of methods).

A ray tracing system relies on acceleration cheme such as bounding volume hierarchy (BVH) to accelerate visibility testing. Generated results have to be treated with denoising algorithms.

how to shadow area lights (where penumbra becomes very important, and function of the area)

ambient occlusion should be applied to all diffuse indirect lighting (e.g. env irradiance) e.g. 11.25 It might be even better to use ambient obscurance.

Better structure mental representation of diffuse(lambertian) vs specular(“glossy”) materials:

Diffuse:
- View independent
- Lambertian BRDF reflects illumination from the entire hemisphere
  - is interested in irradiance
Specualr:
- View dependent
- the evaluation of the reflectance equation needs only lighting incident from a limited solid angle.
  - input is usually radiance

Spatial dithering, look-up “Floyd–Steinberg Dithering”.